kmp算法next计算方法,KMP算法

暴力匹配算法

    假设现在我们面临这样一个问题：有一个文本串S，和一个模式串P，现在要查找P在S中的位置，怎么查找呢？

    如果用暴力匹配的思路，并假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置，则有：

• 如果当前字符匹配成功（即S[i] == P[j]），则i++，j++，继续匹配下一个字符；
• 如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0。相当于每次匹配失败时，i 回溯，j 被置为0。

    理清楚了暴力匹配算法的流程及内在的逻辑，咱们可以写出暴力匹配的代码，如下：

int ViolentMatch(char* s, char* p)
{
    int sLen = strlen(s);
    int pLen = strlen(p);

    int i = 0;
    int j = 0;
    while (i < sLen && j < pLen)
    {
        if (s[i] == p[j])
        {
            //①如果当前字符匹配成功（即S[i] == P[j]），则i++，j++    
            i++;
            j++;
        }
        else
        {
            //②如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0    
            i = i - j + 1;
            j = 0;
        }
    }
    //匹配成功，返回模式串p在文本串s中的位置，否则返回-1
    if (j == pLen)
        return i - j;
    else
        return -1;
}

    举个例子，如果给定文本串S“BBC ABCDAB ABCDABCDABDE”，和模式串P“ABCDABD”，现在要拿模式串P去跟文本串S匹配，整个过程如下所示：

    1. S[0]为B，P[0]为A，不匹配，执行第②条指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，S[1]跟P[0]匹配，相当于模式串要往右移动一位（i=1，j=0）

    2. S[1]跟P[0]还是不匹配，继续执行第②条指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，S[2]跟P[0]匹配（i=2，j=0），从而模式串不断的向右移动一位（不断的执行“令i = i - (j - 1)，j = 0”，i从2变到4，j一直为0）

    3. 直到S[4]跟P[0]匹配成功（i=4，j=0），此时按照上面的暴力匹配算法的思路，转而执行第①条指令：“如果当前字符匹配成功（即S[i] == P[j]），则i++，j++”，可得S[i]为S[5]，P[j]为P[1]，即接下来S[5]跟P[1]匹配（i=5，j=1）

 

    4. S[5]跟P[1]匹配成功，继续执行第①条指令：“如果当前字符匹配成功（即S[i] == P[j]），则i++，j++”，得到S[6]跟P[2]匹配（i=6，j=2），如此进行下去

 

    5. 直到S[10]为空格字符，P[6]为字符D（i=10，j=6），因为不匹配，重新执行第②条指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，相当于S[5]跟P[0]匹配（i=5，j=0）

 

    6. 至此，我们可以看到，如果按照暴力匹配算法的思路，尽管之前文本串和模式串已经分别匹配到了S[9]、P[5]，但因为S[10]跟P[6]不匹配，所以文本串回溯到S[5]，模式串回溯到P[0]，从而让S[5]跟P[0]匹配。

    而S[5]肯定跟P[0]失配。为什么呢？因为在之前第4步匹配中，我们已经得知S[5] = P[1] = B，而P[0] = A，即P[1] != P[0]，故S[5]必定不等于P[0]，所以回溯过去必然会导致失配。那有没有一种算法，让i 不往回退，只需要移动j 即可呢？

    答案是肯定的。这种算法就是本文的主旨KMP算法，它利用之前已经部分匹配这个有效信息，保持i 不回溯，通过修改j 的位置，让模式串尽量地移动到有效的位置。

KMP

1. kmp算法

Knuth-Morris-Pratt 字符串查找算法，简称为 “KMP 算法”，常用于在一个文本串 S 内查找一个模式串 P 的出现位置 俩指针 文本字符串 的指针不往前移动 不回溯

相对比 bf(暴力)算法 利用空间换时间 记录需要对比的字符串中的重复字符串来判断不匹配的时候 (next) 需要将对比字符串的指针往后移动多少 全部不重复的话则表示 直接移动道最开始 最主要是 next 数组来判断不匹配的时候 需要将指针移到什么位置

2. 匹配过程

在模拟 KMP 匹配过程之前，我们先建立两个概念：[next数组后面会有提起， 先不关心怎么来的]

• 前缀：对于字符串 abcxxxxefg，我们称 abc 属于 abcxxxxefg 的某个前缀。
• 后缀：对于字符串 abcxxxxefg，我们称 efg 属于 abcxxxxefg 的某个后缀。
• 假设: 字符串为abcxxxxxxabc, 那么我们称 abc 属于公共前后缀 kmp算法就是用到了这个公共前后缀

首先看第一轮比较

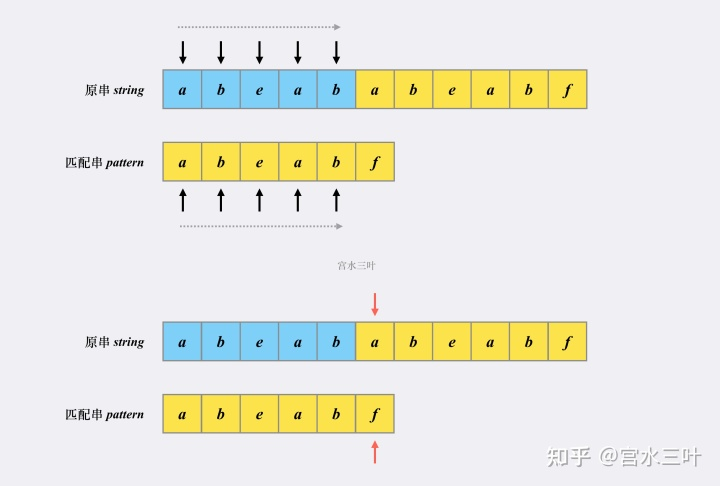
由上图可知 abeabf 先不看f(失配位置 以下称失配字符) 可以看出来 其中最长的前后缀相同的字符是 ab kmp算法说让前面那个 ab 移动到后面 ab的位置也就是因为我们能确保这样是移动最长的 而且主串与模式穿失配字符前面模式串和对应主串全是匹配的 那么我们就是匹配之前主串的失配字符和 最长相同前后缀的前缀的后面一个字符相比较

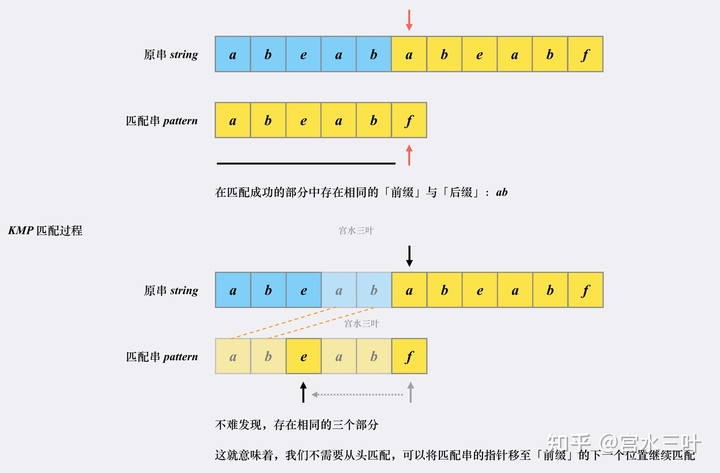
• 因为 KMP 利用已匹配部分中相同的「前缀」和「后缀」来加速下一次的匹配。
• 因为 KMP 的原串指针不会进行回溯（没有朴素匹配中回到下一个「发起点」的过程）。

function kmp(text, tem) {
  const len = text.length;
  const next = [-1, 0, 0, 0, 1, 0];
  let tIndex = 0,
    mIndex = 0;
  while (tIndex < len && mIndex < tem.length) {
    if (mIndex === -1 || text[tIndex] === tem[mIndex]) {
      tIndex++;
      mIndex++;
    } else {
      mIndex = next[mIndex];
    }
  }
  console.log(mIndex === tem.length);
}

那么我们怎么知道 怎么能挑到最长前缀那呢 这就用到了next数组 也叫前缀表

1. 寻找最长前缀后缀

   1. 如果给定的模式串是：“ABCDABD”，从左至右遍历整个模式串

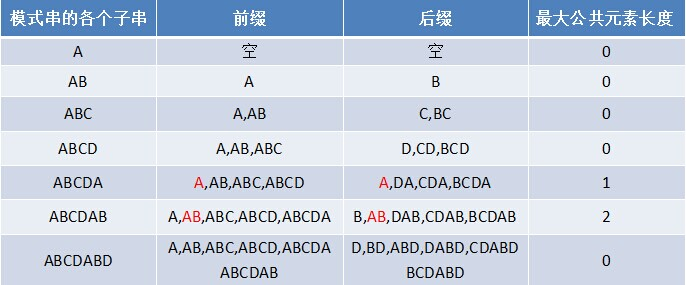
   2. 原模式串子串对应的各个前缀后缀的公共元素的最大长度表

2. 基于《最大长度表》匹配

   字符的上一位字符所对应的最大长度值

    上文利用这个表和结论进行匹配时，我们发现，当匹配到一个字符失配时，其实没必要考虑当前失配的字符，更何况我们每次失配时，都是看的失配字符的上一位字符对应的最大长度值。如此，便引出了 next 数组。
    给定字符串“ABCDABD”，可求得它的 next 数组如下：
   
    ![image.png](https://cyc-save.oss-cn-shanghai.aliyuncs.com/cyc-save/16450819587460.603112059677011.png)
   

3. next数组版本 【1. 整体后移一位 找的时候找模式串失配的位置的下标即可， 2. 整体不动 失配的时候找模式串上一个字符的位置对应的下标 本次以第一种】

4. next 构建 接下来，我们看看 next 数组是如何在 O(m)的复杂度内被预处理出来的。 假设有匹配串 aaabbab，我们来看看对应的 next 是如何被构建出来的。

相同 匹配上的 接下来

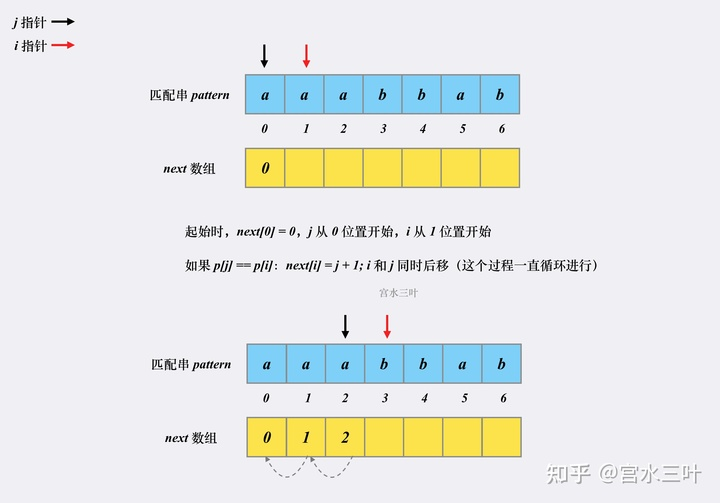
不相同字符

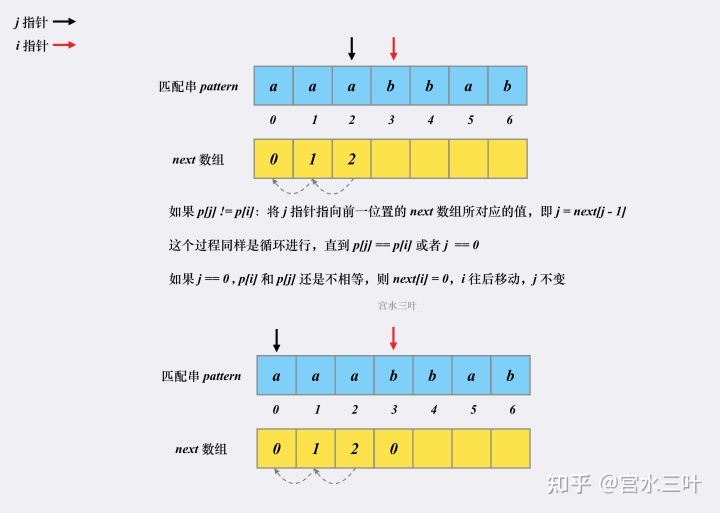
回溯模式串

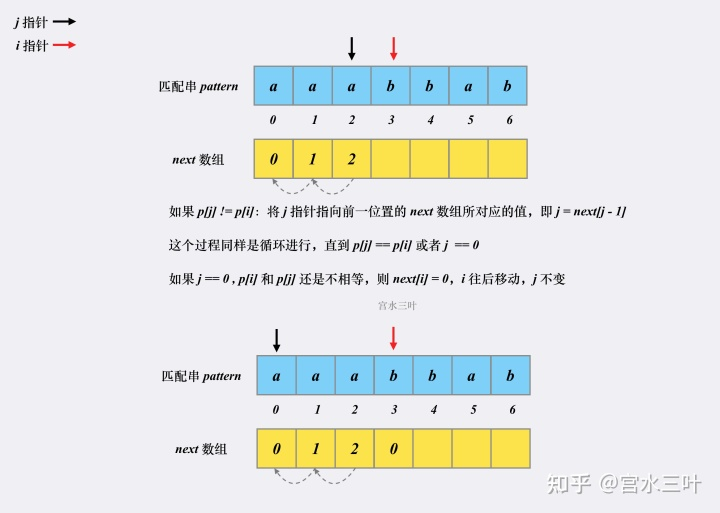
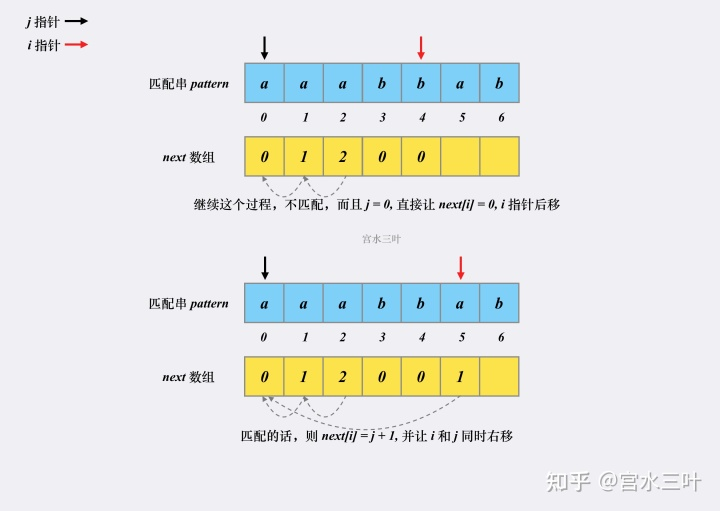
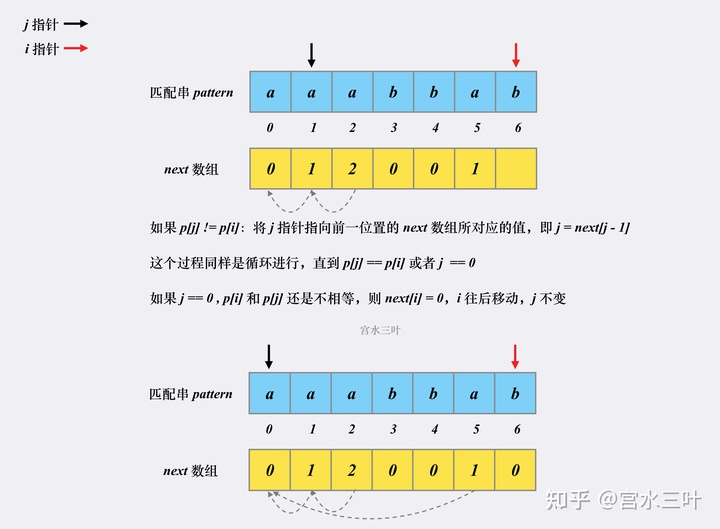
1. next 代码

     ```javascript
    function getNext(p) {
        const next = [-1];
        const len = p.length;
        let l = -1;
        let r = 0;
        while (r < len - 1) {
          if (l === -1 || p[l] === p[r]) {
            l++;
            r++;
            next[r] = l;
          } else {
            l = next[l];
          }
        }
        return next;
      }
    ```
   

“KMP的算法流程：

假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++，继续匹配下一个字符；

如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串P相对于文本串S向右移动了j - next [j] 位。” 我们发现如果某个字符匹配成功，模式串首字符的位置保持不动，仅仅是i++、j++；如果匹配失配，i 不变（即 i 不回溯），模式串会跳过匹配过的next [j]个字符。整个算法最坏的情况是，当模式串首字符位于i - j的位置时才匹配成功，算法结束。 所以，如果文本串的长度为n，模式串的长度为m，那么匹配过程的时间复杂度为O(n)，算上计算next的O(m)时间，KMP的整体时间复杂度为O(m + n)。

KMP的时间复杂度分析 相信大部分读者读完上文之后，无非是循序渐进把握好下面几点：

如果模式串中存在相同前缀和后缀，即pj-k pj-k+1, ..., pj-1 = p0 p1, ..., pk-1，那么在pj跟si失配后，让模式串的前缀p0 p1...pk-1对应着文本串si-k si-k+1...si-1，而后让pk跟si继续匹配。 之前本应是pj跟si匹配，结果失配了，失配后，令pk跟si匹配，相当于j 变成了k，模式串向右移动j - k位。 因为k 的值是可变的，所以我们用next[j]表示j处字符失配后，下一次匹配模式串应该跳到的位置。换言之，失配前是j，pj跟si失配时，用p[ next[j] ]继续跟si匹配，相当于j变成了next[j]，所以，j = next[j]，等价于把模式串向右移动j - next [j] 位。 而next[j]应该等于多少呢？next[j]的值由j 之前的模式串子串中有多大长度的相同前缀后缀所决定，如果j 之前的模式串子串中（不含j）有最大长度为k的相同前缀后缀，那么next [j] = k。

以上图由大佬提供 参考